Making an RISC-V OS (Part 3): Managing free memory

See previous part on handling the transition from physical to virtual memory.

Where is my RAM, and how much of it have I?

When we left last time our kernel had booted up in virtual memory, but we still had no idea what our surroundings looked like. The only things we know about are the sections that have been allocated by the linker in our ELF binary, but those are statically defined, they don't adapt to our hardware.

We need to find a way to get a list of all the devices & memory regions we have access to, with their properties & physical locations. In x86 machines this is often done through ACPI. On RISC-V, as well as ARM, this is often done through Devicetrees.

Device trees are a data structure that is populated by a low-level firmware (or it could even be hard-coded somewhere in the address-space) that contain all the information on the system. Device trees have two main representations:

• A textual format (.dts) that is human editable.
• A binary format (.dtb) that is space efficient and easily parsable by machines.

In order to gather our system specs we are going to rely on the dtb structure populated by QEMU before the system boot. This structure is passed in the a1 register, and OpenSBI forwards it to us.

Looking at the QEMU Devicetree

We can dump the QEMU device tree blob by running qemu-system-riscv64 -M virt,dumpdtb=virt.dtb. It is then possible to convert it to a textual format by running dtc -I dtb -O dts virt.dtb >> virt.dts.

Here is a small extract from the Devicetree with the properties that we want to query for now:

/dts-v1/

/ {
    #address-cells = <0x02>;
    #size-cells = <0x02>;
    compatible = "riscv-virtio";
    model = "riscv-virtio,qemu";

    /* some nodes ... */

    memory@80000000 {
        device_type = "memory";
        reg = <0x00 0x80000000 0x00 0x80000000>;
    };

    /* ... more nodes */
};

The RAM location in physical memory and its length is coded in the reg property of the memory@80000000 node. We simply need to parse this device tree when booting, and we would be able to initialize the rest of the memory.

Parsing the DTB

The Devicetree specification PDF describes in the 5th section the format of the Devicetree.

In summary a device tree is divided in two main sections:

• The struct section, containing the hierarchy of the device tree.
• The strings section, containing the value of numerous properties.

The main structure to be parsed is the struct section, as the strings section is only pointed to. The struct section in organised in nested arrays, each array is composed of the following parts:

• A header indicating the start of a node
• A number of properties of the current object
• A number of sub arrays (each of exactly the same format)
• An end of node marker

This means that to get the offset of the second child of a node the entire first child tree must be parsed. In order to query the Devicetree without needing to re-parse the entire tree each time we can use a new structure of the form:

#[derive(Debug)]
pub struct DeviceTreeNode<'a, 'd> {
    pub name: &'d str,
    // This is a type reprensenting each possible property
    pub props: Vec<'a, DtProp<'a, 'd>>,
    pub children: Vec<'a, DeviceTreeNode<'a, 'd>>,
}

The only issue with this representation is that it requires an allocator, but we are trying to find the RAM, so we don't have any free memory right now!

Note that all integers are stored big-endian! Most tokens also need to be 32 bit aligned. There exists a NOP token that needs to be skipped. All those restrictions make the code a bit more complex than it seems with the description, so I won't show include the parsing function in this post, but it is available on the git repository

The early allocator

In order to parse the dtb we are going to create a small section in the binary using the following assembly snippet:

.section .data
.global _early_heap
.align 12
_early_heap:
.rep 1024 * 1024
    .byte 0
.endr

We can then access this zone with the following code:

const EARLY_HEAP_LEN: usize = 1024 * 1024;

extern "C" {
    #[link_name = "_early_heap"]
    static mut EARLY_HEAP: u8;
}

fn kmain(...) -> ! {
    /* ... See previous part ... */

    let early_heap: &[u8] = unsafe {
        core::slice::from_raw_parts_mut(
            addr_of_mut!(EARLY_HEAP) as *mut MaybeUninit<u8>,
            EARLY_HEAP_LEN,
        )
    };

    /* ... parse the dtb ... */
} 

Using this block of memory we have 1 MiB to do whatever we want! We are going to implement a really simple bump allocator with this memory. A bump allocator looks like this:

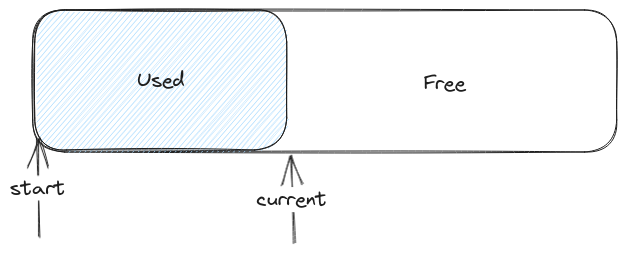
We have a current pointer inside the buffer that indicates when next to allocate. The memory between start and current is in use, and can't be freed. Whenever we need to allocate some memory we can bump the current pointer according to the amount we need, and use that block.

It is possible to improve a bit the bump allocator by implementing two optimizations:

• If are trying to free the last block (meaning the end of the block is equal to current) then we can decrement current by the length of the block. This allows to handle efficiently short-lived objects.
• If we try to re-allocate some memory, and it is the last piece of memory we allocated we can simply bump the current pointer to increase as required the allocation size (or decrease it!). This allows to efficiently implement growable arrays (Vec) where we append the items sequentially, and never touch them again.

Using this allocator we can implement Vec that re-allocate themselves with twice the capacity whenever they are full. This allows us to parse easily the dtb described in the previous section!

Reserved memory

The memory section is not the only useful node to read, there is a second node that is important to locate the RAM: reserved-memory. OpenSBI will reserve some of the RAM for itself, and our OS is not allowed to touch it. This is implemented using Machine level permissions, if we try to access that memory the CPU will trap.

This means that we need to combine the information from the memory field with the information from the reserved-memory field in order to find the effective memory.

Right now Hades only handles a single physical memory block, and uses all memory after the last reserved-memory field.

Allocating (physically contiguous) memory

Now that we know where our physical memory lies we can start to write some code to know what RAM is free, and what RAM is allocated. We are going to write a buddy allocator for getting pages, as it is a quite simple allocator that has nice guarantees on external fragmentation. In order to simplify the implementation we are going to choose the largest allocation size, above which we won't be able to allocate contiguous memory. This is a bit arbitrary, but we are going to choose $2^{12}$ pages or 16 MiB.

A quick aside on fragmentation

When talking about allocators fragmentation is one of the most important things we need to think about. There are two kinds of fragmentation that are important to handle:

• Internal fragmentation
• External fragmentation

External fragmentation measures the "contiguousness" of memory. If an allocator has 16 GiB available, but can't allocate more than 1 KiB of contiguous memory because all the memory is split up, then we would say that the external fragmentation is very large.

Internal fragmentation measures the amount of "wasted" space. An allocator can give a bigger amount of RAM to a request than requested. For example if our allocation is a page (4 KiB), and the user asks for 4 B we would waste most of the space!

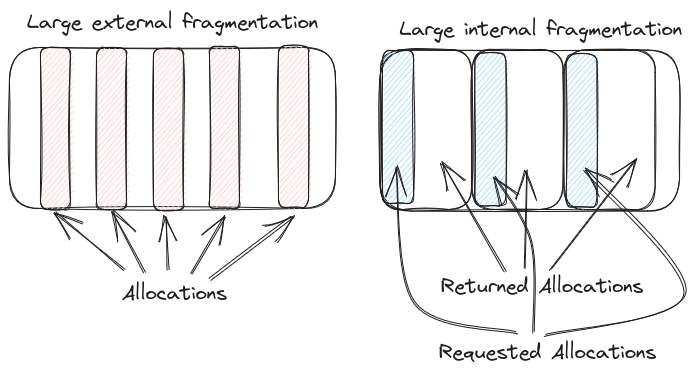
See the Wikipedia page for more details on fragmentation.

Organizing the RAM into free lists

The first step in implementing a buddy allocator is to define free lists for each of the allocation sizes we support. A free list is simply a linked list where we only pop or push to the head of the list. This allows fast access to free elements, if all our elements are fungible.

So we can start our page allocator as follows:

#[derive(Clone, Copy)]
struct FreeList {
    head: Option<&'static Page>,
}

#[derive(Clone, Copy)]
struct FreePageState {
    next: Option<&'static Page>,
}

pub union PageState {
    free: FreePageState,
}

#[derive(Debug)]
#[non_exhaustive]
pub struct Page {
    pub state: UnsafeCell<PageState>,
    /// Represents the status of allocations in the buddy allocator
    allocated: AtomicU16,
}

pub struct PageAllocator {
    free: [FreeList; MAX_ORDER + 1], // MAX_ORDER is 12
    pages: &'static [Page],
}

static PAGE_ALLOCATOR: SpinLock<PageAllocator> = SpinLock::new(PageAllocator {
    free: [FreeList { head: None }; MAX_ORDER + 1],
    pages: &[],
});

We need to initialize the PageAllocator with a pointer to a memory region that will store our bookkeeping for the pages (the array of Page). In our OS we are going to put this at the start of RAM (as found in the dtb). Each entry in the PageAllocator.pages field represents the corresponding 4 KiB page from the remaining of RAM.

The Page structs are linked together using the Page.state.free.next field. This field is only valid when the page is not currently allocated. Because we must use one Page struct for every page in the system it is important to keep the struct as small as possible.

Because there is no way to construct a PageAllocator, as the fields are private, the safety invariants on the PageState rely on the PAGE_ALLOCATOR structure being only accessible through a SpinLock. This allows us to ensure that while we hold the lock we can be sure that there can't be another user that can access unallocated pages, and as such it is safe to take a (single!) mutable reference on the Page.state field.

We are then going to create a init function, that will assign physical memory the to PAGE_ALLOCATOR static:

fn align(v: usize, exp: usize) -> usize {
    assert!(exp.is_power_of_two());

    (v + exp - 1) & !(exp - 1)
}

/// SAFETY: `start` must point to currently _unused_ physical memory
///
/// This function may only be called once
pub unsafe fn init(start: usize, mut length: usize) {
    static INIT: AtomicBool = AtomicBool::new(false);

    assert!(!INIT.load(atomic::Ordering::Relaxed));

    let max_page_size = PAGE_SIZE * (1 << MAX_ORDER);

    let start_aligned = align(start, max_page_size);

    // Remove start pages that are not aligned
    length -= start_aligned - start;
    // Remove end pages that don't fit in a max_page_size
    length -= length % max_page_size;

    // We know know exactly how many 2**12 contiguous pages blocks are available on the system
    let max_page_count = length / max_page_size;

    let page_count = length / PAGE_SIZE;
    let page_info_size = page_count * core::mem::size_of::<Page>();
    let required_pages_for_page_struct = page_info_size.div_ceil(max_page_size);

    // We reserve the start of RAM for our array of Page
    let pages: &[Page] = unsafe {
        core::slice::from_raw_parts(
            (start_aligned + RAM_VIRTUAL_START as usize) as *const _,
            page_count,
        )
    };

    // We iterate over each of the pages in the start of a 2**12 block of pages, 
    // and add it to the max order freelist
    let mut free_pages = [FreeList { head: None }; MAX_ORDER + 1];
    for i in (required_pages_for_page_struct..max_page_count).rev() {
        let page_idx = i * (1 << MAX_ORDER);

        free_pages[MAX_ORDER].add(&pages[page_idx]);
    }

    let mut allocator = PAGE_ALLOCATOR.lock();

    allocator.free = free_pages;
    allocator.pages = pages;

    INIT.store(true, atomic::Ordering::Relaxed);
}

Managing buddy allocations

To represent a page allocation we are going to use a PageAllocation structure, that acts as a RAII handle:

pub struct PageAllocation(&'static [Page]);

impl Deref for PageAllocation {
    type Target = [Page];

    fn deref(&self) -> &Self::Target {
        self.0
    }
}

impl Drop for PageAllocation {
    fn drop(&mut self) {
        PAGE_ALLOCATOR.lock().free(self.0);
    }
}

pub fn alloc_pages(order: usize) -> Option<PageAllocation> {
    if order > MAX_ORDER {
        return None;
    }

    let pages = PAGE_ALLOCATOR.lock().alloc(order)?;

    Some(PageAllocation(pages))
}

We are now going to describe how to allocate & free memory with a buddy allocator!

Page allocation

Allocations with a buddy allocator are quite simple: When allocating an order $n$ we look if we have any available memory in the free list at index $n$ of our PAGE_ALLOCATOR. If a page is available then we remove it from the free list, and return it. If no page is available we try to allocate a page of order $n+1$, and then split it in two parts (the two buddies!), adding the second half to the free list of index $n$ and returning the first half.

Note that this is a recursive algorithm, and it terminates whenever we can allocate a page at a given order because the free list is not empty, or when the free list at index MAX_ORDER is empty, and we try to pop from it.

Here is the code to implement this algorithm:

impl PageAllocator {
    fn alloc(&mut self, order: usize) -> Option<&'static [Page]> {
        match self.free[order].head.take() {
            Some(h) => {
                self.free[order].head = unsafe { (*h.state.get()).free.next };

                h.allocated.fetch_or(1 << order, atomic::Ordering::Relaxed);

                Some(&self.pages[h.index(self.pages)..h.index(self.pages) + (1 << order)])
            }
            None => {
                if order == MAX_ORDER {
                    None
                } else {
                    let larger = self.alloc(order + 1)?;
                    let buddy = &larger[larger.len() / 2];
                    self.free[order].add(buddy);

                    larger[0]
                        .allocated
                        .fetch_or(1 << order, atomic::Ordering::Relaxed);

                    Some(&larger[0..larger.len() / 2])
                }
            }
        }
    }
}

Freeing allocations

Freeing allocations is conceptually simple, but requires a bit more code to implement. The main idea is that when we free a page of order $n$ we try to see if the buddy (meaning the part that was split up during the allocation) is free too. If both are free then we can merge the two pages of order $n$ to create a page of order $n+1$.

We can then recursively free the page of order $n+1$, until we arrive at a page of order MAX_ORDER, where we don't have buddies anymore.

The code that does this is the following:

impl PageAllocator {
    fn free(&mut self, pages: &'static [Page]) {
        // Because order is a power of two this is guaranteed to give the log2
        let order = pages.len().trailing_zeros() as usize;

        // Mark the page as free
        let prev = pages[0]
            .allocated
            .fetch_and(!(1 << order), atomic::Ordering::Relaxed);
        assert!(prev & (1 << order) != 0);

        // If it's a max order page no merging to be done
        if order < MAX_ORDER {
            /// Calculate the index of the page using the address of pages[0]
            let index = pages[0].index(self.pages);
            // Is this the first page or the second page?
            //
            // There exists a trick to find the buddy with a bit manipulation if sizes are a 
            // power of two, but as I don't exactly understand it I have not implemented it
            let (first_idx, buddy_index) = match index % (1 << (order + 1)) {
                0 => (index, index + (1 << order)),
                _ => {
                    let first = index - (1 << order);
                    (first, first)
                }
            };

            let buddy = &self.pages[buddy_index];
            // Find if the buddy is currently allocated
            let buddy_allocation = buddy.allocated.load(atomic::Ordering::Relaxed);

            if buddy_allocation & (1 << order) == 0 {
                // Remove the buddy from it's freelist. Because we use a simply linked list we need
                // to iterate over the list to it.
                // I may implement a doubly linked list at a further date to alleviate this, but
                // it is much more unsafe to do in rust
                self.free[order]
                    .remove(buddy)
                    .expect("buddy was not in the free list while it was un-allocated");

                buddy
                    .allocated
                    .fetch_and(!(1 << order), atomic::Ordering::Relaxed);

                // Recursively free the aggregated large page
                return self.free(&self.pages[first_idx..first_idx + (1 << (order + 1))]);
            }
        }

        self.free[order].add(&pages[0]);
    }
}

With this we can now handle allocations & de-allocations of blocks of pages, up to 16 MiB. Note while the buddy allocator handles external fragmentation well (due to us always re-aggregating the memory), our allocator has issues with internal fragmentation. Indeed, even if we need to allocate a single byte we need to allocate a 4 KiB page! This is often solved using slab allocators, but we won't be implementing one right now, as we try to keep the complexity to a minimum if we don't encounter any issues.

Next you can follow a long side quest needed before we implement a pretty neat feature for our kernel!